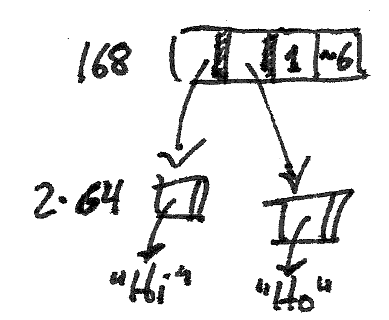
When I first stumbled on Dan Bernstein's description of crit-bit trees, I got really excited.³ He paints a pretty compelling picture: a data structure simpler, faster, smaller, and more featureful than hash tables. Who needs these hash tables anyway?

Of course, it turned out that in practice, at least for the critbit trees described by djb, all that pointer-chasing wasn't great, and it's not straightforward to adapt to types where you don't have a natural sentinel like NUL.

Then I found Tony Finch's qp-tries which are even better, but first let's go through HAMT.

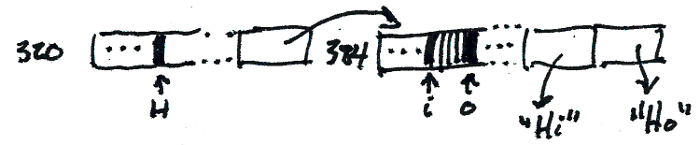
Marek's introduction to HAMT is better at explaining this than I am, but briefly: there's this great trick you can do if you have a fast way to count the 1s in a bitmap (this operation is called population count, or "popcount" for short).⁴

Let's say you want a map from the integers [0,8) to elements in an array. This is such a small number that you could just allocate eight elements and your "map" is just array indexing, but let's pretend eight is a larger number, since I didn't want to draw a bunch of sixty-four-element-wide diagrams in this article.

If you wanted to only allocate space for the elements that are present in this map, you could use an 8-bit bitmap to indicate presence, and store the elements in order. Now, popcount of the whole bitmap gives you the number of elements present; the individual bits tell you a given element is present; and the popcount of the bitmap masked by the bits lower than that element gives you its index in the array.

Phil Bagwell presents this idea in Fast and Efficient Trie Searches to yield array mapped tries (AMT)⁵. Later, in Ideal Hash Tries, he builds on these to yield hash array mapped tries (HAMT), which have become widely implemented.^{6 , 7}

This popcount trick appears in all sorts of other places, for example in unrelated travels I just ran into it in the Caroline Word Graph as a consequence of reading Appel and Jacobson's The World's Fastest Scrabble Program. (Which I now notice is also cited by Bagwell in the aforementioned paper.)

(BTW, Bagwell's other papers, such as Fast Functional Lists, are also well worth reading!)

Now, qp-tries sort of combine HAMT and crit-bit trees; they work with larger chunks instead of a bit at a time; the original description was a nibble at a time, so a 64-bit word uses 16 bits for a bitmap representing possible nibbles, and the rest of the word stores the index of the nibble being tested (the "critical nibble").

I found qp-tries inspiring in part because of the lucid implementation which yielded great performance with simple code. Check out qp.h for a nice overview in the comments, and qp.c for the implementation.

qp-tries are great for lots of cases, especially strings; I wanted to go on about them but in general I suggest just checking out everything on the qp-trie homepage.

For whatever reason, this never came to me when I encountered HAMT, but my ears perked up when I heard 16, 48, 64, in the description of qp-tries. In practice, x86-64 machines only use 48 of the bits in a pointer (64 bits); what about the other 16? Intel has the following to say about addresses: (SDM volume 1, 3.3.7.1 Canonical Addressing)

In 64-bit mode, an address is considered to be in canonical form if address bits 63 through to the most-significant implemented bit by the microarchitecture are set to either all ones or all zeros.

Intel 64 architecture defines a 64-bit linear address. Implementations can support less. The first implementation of IA-32 processors with Intel 64 architecture supports a 48-bit linear address. This means a canonical address must have bits 63 through 48 set to zeros or ones (depending on whether bit 47 is a zero or one).

Although implementations may not use all 64 bits of the linear address, they should check bits 63 through the most-significant implemented bit to see if the address is in canonical form. If a linear-memory reference is not in canonical form, the implementation should generate an exception.

(Note this means that pointers are in a sense "signed" on this platform!)

So, we get no guarantees that we can always use those upper 16 bits, but this is the case presently⁸: they must always be all zeros, or all ones. And, at least on Linux, the kernel uses the "negative" addresses (whose 16-bit prefix is all ones), so our userspace pointers are always zero there. What a tempting place to stuff some extra data!

Then, earlier this year, I was laying the groundwork for potentially developing a service in Rust at a company where previously such services had been written in C. I wanted to write some code that would prove to me that it wouldn't be too painful to drop to the level of pointers, bits, and syscalls that we needed. I started with the magic ringbuffer, and then a popcount-based tiny compact map.⁹

Finally, I needed a structure where I could space-efficiently map fixed-length integers to values. What if we gave up critbit's nice property of compressing paths where the bits are the same, and reconstructed the key by traversing the trie? Could we stuff that bitmap into the unused bits, and end up with a single word per branch?

That's basically fixie tries: we use the lowest bit on a pointer to determine if it's a branch or a leaf (since pointers must be word aligned, we actually have a few free bits at the bottom). If it's a branch, we cut off its sign extension and put a bitmap there; the pointer that results from masking the branch with 0x0000_ffff_ffff_fffe points to an array containing the children indicated by the bitmap.

If a leaf is at the deepest level in the trie, it just points directly to a value, since we can reconstruct the key as we walk to it. If the leaf is somewhere shallower, we store a tuple of the full key and the value; there are probably improvements to be made there, but the hassles of aligning a partially-nibbled key have kept me away from them.

To be clear, though qp-tries were what sparked the flame, these are more like Bagwell's array mapped tries. They're x86-64-specific¹⁰, in a way that you probably don't want to depend on, and they're not magically better than everything else, but they have a few nice properties.

Sadly I mostly had a puny AMD E-350 to benchmark this on, but thankfully a friend ran it on a machine identifying itself as packing 16 × Intel(R) Core(TM) i7-7820X CPU @ 3.60GHz.

Random insertions of 32-bit keys as a set: (it would be nice to add Roaring or similar to this benchmark)

test random_u32_insertions_on_hash_set          ... bench:         134 ns/iter (+/- 139)
test random_u32_insertions_on_fixie_trie_as_set ... bench:         293 ns/iter (+/- 26)
test random_u32_insertions_on_btree_set         ... bench:         343 ns/iter (+/- 44)

Random insertions of 64-bit keys and 32-bit values:

test random_u64_insertions_on_hash_map          ... bench:         154 ns/iter (+/- 158)
test random_u64_insertions_on_fixie_trie_as_map ... bench:         266 ns/iter (+/- 32)
test random_u64_insertions_on_btree_map         ... bench:         435 ns/iter (+/- 44)

One thing that's part of djb's argument for critbit trees that remains true for fixie tries is relatively uniform performance. We can see that hash inserts are fast, but have a lot of variance.

Random queries on 32-bit keys, acting as a set:

test u32_random_queries_on_btree_set               ... bench:           5 ns/iter (+/- 0)
test u32_random_queries_on_fixie_trie_set          ... bench:          22 ns/iter (+/- 0)
test u32_random_queries_on_hash_set                ... bench:          29 ns/iter (+/- 0)
test u32_random_queries_on_a_qp_trie_set           ... bench:          59 ns/iter (+/- 0)

I was surprised by how good BTreeSet is here; some of my early benchmarking (at the beginning of the year) indicated otherwise, but it (or my methodology) must have improved.

Random queries on 64-bit keys for 32-bit values:

test u64_random_queries_on_fixie_trie              ... bench:          23 ns/iter (+/- 0)
test u64_random_queries_on_hash_map                ... bench:          31 ns/iter (+/- 0)
test u64_random_queries_on_btree_map               ... bench:          93 ns/iter (+/- 1)

BTreeMap starts to fall behind as the key size grows here.

Memory usage (maximum RSS of process) after random insert of n 64-bit keys associated with 32-bit values:

As we can see, BTreeMap is actually quite compact, which I didn't expect; since we're measuring the whole process's usage, this takes into account allocator fragmentation and so on. It's likely that with a custom allocator, fixie tries would be much more compact.

Overall, despite still having a lot of relatively low-hanging optimization opportunities, fixie tries do ok here: they use much less memory than hash maps and qp-tries, and have consistent performance for inserts and queries that is never slower than the alternatives tested.

Aside from the regular disclaimers, here's something specific to how this benchmark is written. What's wrong with this approach?

let mut rng = rand::thread_rng();
let mut t = FixieTrie::new();
b.iter(|| {
    for _ in 0..N_INSERTS { t.insert(rng.gen::<u32>(), ()); }
});

It makes fixie tries look great compared to BTreeSets. You should always scrutinize a benchmark, especially when it surprises you, but most of all when it confirms your own beliefs (or desires). This is when it is most tempting to stop looking and publish your results. (This making it a rhetorical benchmark.)

We don't recreate the trie every time in this test, so the trie gets progressively fuller as the iterations continue. Maybe fixie tries are good in this situation, but it's not what we meant to test, and isn't likely to give us much accuracy since the real workload will change every iteration.

Unfortunately, cargo bench doesn't give us the ability to do any kind of setup/teardown between iterations, so we're forced to use patterns like this:

fn random_insertions_on_a_set<T: Rand, S: Set<T>>(b: &mut Bencher, new: fn () -> S)
{
    let mut rng = rand::thread_rng();
    let mut s = new();
    for _ in 0..N_INSERTS { s.insert(rng.gen()); }
    b.iter(|| { s.insert(rng.gen()); });
}

I can't fault cargo bench too much here, because it does so much right, out of the box: it warms up the code under test before trying to measure, and uses somewhat robust statistical measures to determine when it's safe to stop (rather than using the mean and standard deviation as you'll see in a lot of benchmarks). Also, it takes a lot of fiddly, system-specific code to be able to measure a single iteration with accuracy, so it would be difficult for it to provide this interface.

But since the underlying structure is changing on every iteration, we may not be measuring what we think we're measuring. At least filling it partially before starting the timing puts the inserts-under-measurement in more consistent territory.

After updating this crate to use the latest Rust allocator API, some tests would hang. Digging in with gdb revealed they were deadlocked, trying to lock a mutex they already held. Although I was 99% sure this was a bug in my code, jemalloc has had its fair share of deadlock bugs in the past so I held a glimmer of hope I could find something really interesting.

The tests didn't hang with the system allocator and valgrind saw nothing wrong. So I dug into the code and learned a lot about jemalloc's internals; especially I learned that there's a lot of tricky locking in the thread cache code, which surprises me since the point of the thread cache is to reduce synchronization overhead, but I guess I was looking at all the slow paths. I observed that modifying lg_tcache_max (the largest size-class kept in the thread cache) changed at what point it deadlocked, but not in a predictable way (making a table of values to progress, there was a general trend that the larger the classes allowed, the more progress it made, but not consistently).

One of the interesting things was how predictable the failure was. Thinking I might be doing something to corrupt jemalloc's structures badly enough to corrupt the lock, I scripted gdb to print the state of the lock at the points where it was locked and unlocked in the function where it deadlocks, which revealed that the locks looked fine in that function. Unfortunately, because everything was optimized out, it was hard to introspect the structures I thought might have been getting corrupted; I started building rust with a debug, assertion-laden jemalloc, but I knew it would take all night on my laptop.

Before I called it a night, I scripted gdb to print all the calls to mallocx, rallocx, and sdallocx, and their return values, and started putting together a sed script to transform this into a C program that made the same sequence of allocations and deallocations.¹¹

When I woke up the next morning, I realized there was something suspicious about the deallocations logged. I tested with the system allocator, but with various allocators LD_PRELOAD'd, including the same version of jemalloc that Rust was using; none of these hung. So I asked myself, what's the difference?

Of course, Rust is using the sized deallocation API (sdallocx), and the system allocator will be going through malloc and free and not passing any sizes. Looking again at how my library was calling dealloc, I spotted the bug instantly; I was claiming some things I was freeing were smaller than they actually were. Changing this fixed the bug. I took a look through the paths that sdallocx would take if given smaller sizes, and it looks like if my build of Rust with jemalloc assertions enabled had finished compiling, it would have detected my mistake, but otherwise, supplying the wrong size would cause havoc in the thread cache later.

You might say that I should have known to look at these things first, but such is the nature of bugs.

I would have zero confidence in this if it weren't for property testing. Although not as full-featured as the libraries for some other languages, Rust's quickcheck is extremely easy to integrate into the development process, and found tons of bugs that my own, manually-crafted unit tests never would have turned up.

A nice property we have when making a data structure that obeys some common interface is that we can just test against a known-good structure that obeys the same interface:

#[derive(Copy, Clone, Debug)]
enum MapOperation<K: FixedLengthKey, V> {
    Insert(K,V), Remove(K), Query(K),
}

impl<K,V> Arbitrary for MapOperation<K,V>
    where K: Arbitrary + FixedLengthKey + Rand,
          V: Arbitrary + Rand {
    fn arbitrary<G: Gen>(g: &mut G) -> MapOperation<K,V> {
        use self::MapOperation::*;
        match g.gen_range(0,3) {
            0 => Insert(g.gen(), g.gen()),
            1 => Remove(g.gen()),
            2 => Query(g.gen()),
            _ => panic!()
        }
    }
}

quickcheck! {
    // A small keyspace makes it more likely that we'll randomly get
    // keys we've already used; it's easy to never test the insert
    // x/remove x path otherwise.
    fn equivalence_with_map(ops: Vec<MapOperation<u8,u64>>) -> bool {
        use self::MapOperation::*;
        let mut us = FixieTrie::new();
        let mut them = ::std::collections::btree_map::BTreeMap::new();
        for op in ops {
            match op {
                Insert(k, v) => { assert_eq!(us.insert(k, v), them.insert(k, v)) },
                Remove(k) => { assert_eq!(us.remove(&k), them.remove(&k)) },
                Query(k) => { assert_eq!(us.get(&k), them.get(&k)) },
            }
        }
        us.keys().zip(them.keys()).all(|(a,&b)| us.get(&a) == them.get(&b))
    }
}

This allocates a lot, and buffering writes could help, as well as a custom allocator. Bagwell's papers talk about the importance of knowing the common allocation patterns and tailoring the allocator to them.

Dropping the trie is expensive right now. This is something that would be a lot faster with a hierarchical or region-based allocator, as long as the keys and values don't implement Drop; you would much rather throw the whole area away than having to walk it just to dispose of it, which is what I do in the current implementation.

We still have some unused bits in our branch structure. If prefix-compression ended up being useful, it could be stuffed into one of those bits. As it is, though, I like that the pointer structure is pretty simple.

Tony Finch has explored lots of qp-trie variants; some of the same ideas are also applicable to fixie tries. Prefetching made a noticeable difference for qp-tries.

There are some interesting concurrent tries in the same vein, including CTries, and to a lesser extent poptries. I thought about a reasonable scheme for lockless insertions in fixie tries, but haven't had time to implement it.

It might be nice to do something like direct pointing, also from poptries, where the first n bits are covered by a 2ⁿ array of tries. This is a little reminiscent of the two-level approach of Roaring bitmaps.

Finally, there are still a lot of interface niceties missing from this. For example, it really should implement Entry but I haven't gotten around to it yet.

Let me know if you end up using fixie tries or just end up taking inspiration from this world of trie techniques to build you own little trie variant.